

| Matrix-Column Representations of Symmetry Operations |
|
The matrix representation of a symmetry operation is given in its matrix-column pair: (W, w) where W is a 3x3 matrix called the rotational part or matrix part; and w is a 3x1 vector called the translation part or column part. In crystallography in general, an efficient procedure is applied to condense the description of symmetry operations by matrix-column pairs considerably. The so-called short-hand notation of the matrix-column pair (W, w) consists of a coordinate triplet. The following examples illustrate the assignments of the coordinate triplets to the matrix-column pairs:
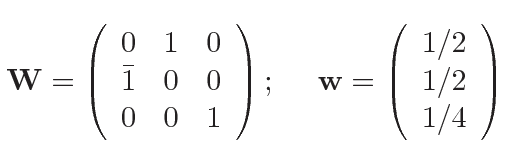 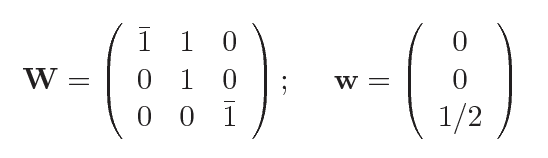 it can be represented in the short-hand notation by the coordinate triplet: -x+y, y, -z+1/2 |